Zásady hodnocení celistvosti konstrukcí při poškození - II
Druhá část článku dokončuje popis metodiky hodnocení celistvosti (robustnosti, integrity) stavebních konstrukcí (úvodní část byla uveřejněna v minulém čísle 9/2010). Použití metodiky je ukázáno na numerickém příkladu rozhodování na základě optimalizace nákladů.
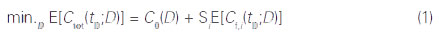
Absolvoval FAST ČVUT v Praze, PhD. získal na University of Waterloo v Kanadě. Od roku 2002 je profesorem na ČVUT v Praze. V roce 2009 byl jmenován mimořádným profesorem na University of Stellenbosch, JAR. Pracuje v řadě národních a mezinárodních odborných komisí v oblasti výzkumu a normalizace (CIB, IABSE, RILEM JCSS, ISO/TC 98, CEN/TC 250). Je předsedou Technické normalizační komise TNK 38 Spolehlivost stavebních konstrukcí. Je delegátem ČR v Evropském výboru pro normalizaci CEN v rámci technické komise TC 250 Structural Eurocodes a subkomise TC 250/SC1 Actions on Structures.
Modely konstrukce
Hodnocení celistvosti vyžaduje použití modelů vhodných pro popis chování konstrukce při různých scénářích poškození a pro odhad pravděpodobnosti progresivního kolapsu za předpokladu, že došlo k mimořádné události. Tyto modely by měly být schopné postihnout chování částečně poškozené konstrukce, vznik velkých trhlin, plastické a nadměrné deformace, řetězovkového působení prvků, membránové působení, vliv vysokých teplot, dynamické účinky apod. Pro praktické použití je potřebný rozvoj výpočetních programů ověřených experimenty. Vzhledem k velké výpočetní náročnosti je potřebné navrhnout zjednodušená pravidla, která by bylo možné alternativně použít ve vymezených případech.
Často používaným scénářem poškození je odstranění sloupu nosné konstrukce budovy. Indikativní pravděpodobnosti odstranění jakéhokoliv sloupu v budově pro dané nebezpečí jsou naznačeny v první části článku [1].
Zásady pro navrhování
Vzhledem k velkému množství scénářů nebezpečí, které mohou vést k progresivnímu kolapsu, je obtížné navrhnout obecně použitelný postup zajištění celistvosti. Ke snížení pravděpodobnosti progresivního kolapsu mohou přispět následující konstrukční opatření [2]:
-
tvarová přeurčitost umožňující alternativní přenos zatížení;
-
systémová opatření jako prostorové provázání konstrukce, nebo naopak oslabení vazeb mezi částmi konstrukce;
-
zajištění dostatečné duktility prvků a jejich spojů pro zajištění odolnosti i při velkých deformacích (průhyby a pootočení) a umožnění redistribuce napětí;
-
dostatečná odolnost vzhledem ke křehkým způsobům porušení;
-
vyšší spolehlivost vybraných konstrukčních prvků (sloupy, nosníky, desky) a odolnost k opačně působícím zatížením (např. výbuch může působit opačným směrem než užitné zatížení);
-
vnější sloupy a zdi přenášející zatížení bez ztráty stability i při selhání horizontálních podpěr ve dvou a více podlažích (zřícení několika pater budovy);
-
sloupy odolné účinkům výbuchu;
-
ověření schopnosti konstrukce přenášet zatížení i v případě lokální poruchy;
-
kontrola jakosti a kvality pro omezení lidských chyb;
-
dostatečná údržba.
V dánském předpisu DS-INF 146 [3] je celistvost vztažena ke scénářům nebezpečí a může být dosažena výběrem vhodných materiálů, statického působení konstrukce, konstrukčního uspořádání a zajištěním spolehlivosti klíčových prvků. Klíčový prvek je část konstrukce, která má zásadní význam pro její intenzitu. Jakákoliv porucha tohoto prvku vede ke zřícení konstrukce nebo její významné části. Celistvost je hodnocena prostřednictvím technické zprávy. Dostatečná celistvost je prokázána splněním alespoň jedné z následujících podmínek:
-
Části konstrukce významně ovlivňující spolehlivost mají malou citlivost k neočekávaným zatížením a poruchám.
-
Rozbor scénáře nebezpečí ?odstranění sloupu? prokáže, že k progresivnímu kolapsu nedojde.
-
Je zajištěna dostatečná spolehlivost klíčových prvků.
Opatření pro zajištění celistvosti betonových konstrukcí jsou popsána v článku [4].
Rozhodování o opatřeních pro zajištění celistvosti
V době návrhu nemusejí opatření pro zajištění celistvosti zvyšovat významně cenu konstrukce (např. volbou vhodného konstrukčního systému a materiálů s dostatečnou duktilitou). V jiných případech (vedlejší nosné systémy, obnovy existujících konstrukcí) však může dojít k výraznému zvýšení nákladů. Rozhodování o opatřeních by pak měla být založena na optimalizaci celkových nákladů vztažených k návrhové životnosti konstrukce s uvážením přímých i nepřímých následků poruchy. Při optimalizaci se využívají postupy analýzy rizik a pravděpodobnostní optimalizace.
Při rozborech rizik konstrukčních systémů se nejčastěji používají stromkové diagramy a Bayesovské (příčinné) sítě. Stromkové diagramy jsou relativně jednoduchým nástrojem, avšak nevhodným pro popis složitějších závislostí mezi jevy a postupy pravděpodobnostních aktualizací. Tyto nedostatky lze odstranit prostřednictvím Bayesovských sítí, které představují účinný nástroj pro rozbory složitých konstrukčních systémů.
Celkové náklady mohou zahrnovat náklady na výstavbu, provoz, údržbu, prohlídky, opravy, odstávky provozu a očekávané následky poruchy. Často lze předpokládat, že rozhodnutí o opatřeních pro zajištění celistvosti významně neovlivní náklady na provoz, údržbu, prohlídky, opravy a odstávky provozu. Optimální rozhodnutí pak může být stanoveno minimalizací redukovaných celkových nákladů Ctot(tD;D):
![]()
kde Ctot označuje redukované celkové náklady vztažené k návrhové životnosti tD; D rozhodnutí o opatřeních pro zajištění celistvosti; C0 počáteční náklady a Cf,i náklady související s poruchou konstrukce vztažené k tD, závisející na pravděpodobnosti lokální poruchy i. Sumace se provádí s ohledem na všechny nezávislé zatěžovací stavy a způsoby porušení.
Počáteční náklady se skládají z nákladů nezávislých na rozhodnutí (prohlídky, návrh, část nákladů na výstavbu) a nákladů na opatření pro zajištění celistvosti. Následky související s poruchou zahrnují přímé a nepřímé následky. Stanovení následků poruchy je velmi důležitá, avšak také zřejmě nejobtížnější část optimalizace nákladů. Předchozí zkušenosti naznačují, že následky poruchy mohou být odhadnuty s využitím Bayesovských sítí, jak se ukazuje v numerickém příkladu. Počáteční náklady a následky poruchy musí být stanoveny ve stejných jednotkách. Obvykle se volí tzv. současná cena [5]. Následky poruchy, které mohou vzniknout v libovolném časovém okamžiku během návrhové životnosti, je proto potřebné převést na současnou hodnotu prostřednictvím následujícího vztahu:
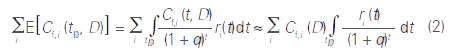
kde Cf,i označuje následky poruchy za předpokladu vzniku lokální poruchy (často časově nezávislé); q roční diskontní sazbu a ri(·) podmíněnou pravděpodobnost vzniku poruchy, nezávislou na rozhodnutí o opatřeních, která je dána vztahem:
![]()
kde F(·) značí lokální poruchu; F doplňkový jev k poruše; (·)’ derivaci podle času a pf(·) pravděpodobnost lokální poruchy vztaženou k referenčnímu období.
Zásady pravděpodobnostní optimalizace jsou podrobněji popsány v článku [5, 6].
Numerický příklad
Numerický příklad ukazuje rozhodování o opatřeních pro zajištění celistvosti na základě optimalizace celkových nákladů. Pro administrativní budovu je efektivnost opatření ověřována s uvážením trvalé a mimořádné návrhové situace způsobené vznikem požáru. Počítá se s vlivem lidských chyb. Zjednodušený rozbor se zaměřuje na hlavní kroky pravděpodobnostního rozboru, analýzy následků a pravděpodobnostní optimalizace.
Pravděpodobnostní rozbor spolehlivosti
Spolehlivost konstrukčního prvku je analyzována prostřednictvím pravděpodobnostních postupů. V trvalé návrhové situaci je prvek vystaven stálému a proměnnému zatížení, v mimořádné návrhové situaci působí stálé zatížení a zatížení vyvolané vznikem požáru. Návrhová životnost je 50 let.
Pravděpodobnost lokální poruchy je sjednocením pravděpodobností poruchy v trvalé návrhové situaci během (0,t) a poruchy způsobené požárem během (0,t). Při rozboru se zjednodušeně použije horní mez pravděpodobnosti poruchy daná součtem:
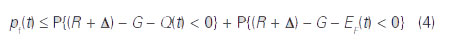
kde R označuje odolnost; Δ vliv lidské chyby (zjednodušeně se uvažuje, že k chybě dojde před dokončením stavby, a je tedy časově nezávislá); G je stálé zatížení; Q maximum proměnného zatížení vztažené k referenční době t a EF účinek zatížení při požáru. Uvažované pravděpodobnostní modely základních veličin jsou uvedeny v tabulce 1, kde jsou statistické charakteristiky normalizovány průměrem odolnosti.
| Veličina |
Symbol |
Rozdělení |
Průměr |
Směrodatná odchylka |
| Odolnost |
R |
normální |
1 |
0,15 |
| Vliv lidské chyby |
Δ| |
normální |
0 |
0,3 |
| Stálé zatížení |
G |
normální |
0,1 |
0,01 |
| Proměnné zatížení (50 let) |
Q50 |
Gumbelovo (max) |
0,13 |
0,028 |
| Zatížení při požáru |
EF|požár |
normální |
0,36 |
0,11 |
¤ Tab. 1 Modely základních veličin
Průměr proměnného zatížení se v závislosti na referenční době t stanoví z následujícího vztahu:

Směrodatná odchylka σQ zůstává konstantní. Pravděpodobnost vzniku nezanedbatelné lidské chyby se odhaduje konzervativní hodnotou 0,2. Počet vzniků požárů se popisuje Poissonovým procesem s parametrem λ = 4×10-4 / rok. Pravděpodobnost alespoň jednoho požáru během t je P (požár|t) = 1 - e-λt, a tedy P (požár|50 let) = 0,02. Pro uvažované modely vede rozbor spolehlivosti k pravděpodobnosti lokální poruchy přibližně 0,004 pro období 50 let, z toho přibližně 70 % připadá na lidskou chybu. Z rozboru vyplývají následující podmíněné pravděpodobnosti lokální poruchy:
-
pf (50 let) = 7×10-5, pokud nedojde k žádné chybě ani rozvinutí požáru, tato pravděpodobnost odpovídá směrné hodnotě indexu spolehlivosti 3,8 pro střední následky poruchy a 50letou referenční dobu (běžné předpoklady pro administrativní budovy),
-
pf = 0,06 za předpokladu vzniku požáru.
Stanovení následků poruchy
Stanovení následků poruchy za předpokladu vzniku lokální poruchy (v důsledku lidské chyby, požáru, nebo trvalé návrhové situace) je založeno na Bayesovské síti znázorněné na obr. 1. Rozhodovací uzel Stupeň provázání má tři stavy popisující nízkou/střední/vysokou úroveň celistvosti zajištěnou provázáním konstrukčních částí. Za předpokladu vzniku lokální poruchy ovlivňuje provázání podmíněné pravděpodobnosti progresivního kolapsu následujícími způsoby:
-
lokální účinky: za předpokladu, že nepříznivé jevy ovlivní jeden nebo menší počet konstrukčních prvků (lokální zatížení), tvarová přeurčitost konstrukce může vést k alternativním přenosům zatížení a části konstrukce neovlivněné poruchou mohou přenést zatížení; vliv opatření je pozitivní;
-
globální účinky: při výskytu jevů, které nepříznivě ovlivní všechny, nebo většinu konstrukčních prvků (chyba při stanovení zatížení v návrhu, zatížení sněhem po celé střeše), může provázání konstrukce přispět k rozvoji progresivního kolapsu.

¤ Obr. 1. Bayesovská síť pro stanovení následků poruchy za předpokladu vzniku lokální poruchy
Vliv stupně provázání na podmíněné pravděpodobnosti progresivního kolapsu je naznačen v tab. 2.
| Stupeň provázání |
Lokální účinky |
Globální účinky |
| Nízký |
0,25 |
0,3 |
| Střední |
0,05 |
0,35 |
| Vysoký |
0,025 |
0,4 |
¤ Tab. 2. Podmíněné pravděpodobnosti progresivního kolapsu za předpokladu vzniku lokální poruchy
Užitkové uzly Společenské a Ekonomické následky popisují následky pro různé situace. Za předpokladu, že vznikne lokální porucha a nedojde k progresivnímu kolapsu, představují ekonomické následky 7,5 % z počátečních nákladů C0 = 40 mil. eur. Při vzniku progresivního kolapsu se odhadují ekonomické následky na čtyřnásobek počátečních nákladů. Předpokládá se, že kolaps způsobí se 75% pravděpodobností 10 úmrtí a s 25% pravděpodobností 50 úmrtí. Náklady na ochranu lidského života v České republice se odhadují na 1 mil. eur [7]. Odhadnuté společenské a ekonomické náklady jsou uvedeny v tab. 3.
| Stupeň provázání |
Lokální účinky |
Globální účinky |
| Nízký |
111 |
131 |
| Střední |
28 |
152 |
| Vysoký |
18 |
173 |
¤ Tab. 3. Společenské a ekonomické následky za předpokladu vzniku lokální poruchy (v mil. eur)
Poznamenáme, že pokud dojde k lokální poruše, odpovídají celkové následky poruchy trojnásobku počátečních nákladů pro lokální účinky a čtyřnásobku pro globální účinky, což odpovídá doporučením v JCSS Probabilistic Model Code [8].
Optimalizace nákladů
Optimální stupeň provázání je dále stanoven prostřednictvím minimalizace celkových nákladů založené na následujících předpokladech.
-
Rozhodnutí významně neovlivní náklady na provoz, údržbu, prohlídky, opravy a odstávky provozu.
-
Počáteční náklady C0 vzrostou o 0,25 % pro střední a o 0,5 % pro vysoký stupeň provázání.
-
Diskontní sazba je 3 %.
Z rovnic (1) až (3) vyplývá následující vztah:
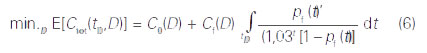
kde Cf(D) označuje následky poruchy podle tab. 3 a pf(·) pravděpodobnost poruchy stanovená z funkce mezního stavu (4).

¤ Obr. 2 Normalizované celkové náklady pro různé stupně provázání a lokální nebo globální účinky
Obr. 2 ukazuje normalizované celkové náklady pro tři stupně provázání a lokální a globální účinky nepříznivých jevů, s uvážením lidských chyb. Navíc je naznačena varianta pro lokální účinky při zanedbání vlivu lidských chyb. Normalizované celkové náklady jsou stanoveny jako rozdíl mezi celkovými a počátečními náklady pro nízkou úroveň provázanosti dělený počátečními náklady. Z obr. 2 vyplývají následující poznatky:
-
pro globální účinky nepříznivých jevů je optimální nízká úroveň provázání;
-
pro lokální účinky a při uvážení lidských chyb vycházejí minimální celkové náklady pro střední úroveň provázání;
-
pokud se zanedbají lidské chyby, je pro lokální účinky optimální nízký stupeň provázání.
Ukazuje se, že lidské chyby a druh účinků nepříznivých jevů ovlivňují optimální rozhodnutí o opatřeních pro zajištění celistvosti. Celkové náklady vzrůstají při uvážení lidských chyb. Poznamenáme, že numerické výsledky jsou založené na předpokladu pravděpodobnosti výskytu hrubé chyby 0,2, což může být poněkud konzervativní hodnota pro běžnou stavební praxi.
Numerické výsledky jsou pouze indikativní. Významně je ovlivňují vstupní údaje pro uzly Úmrtí, Společenské a Ekonomické následky, které by měly být vždy pečlivě stanoveny s ohledem na skutečné podmínky sledované konstrukce. Užitečné informace pro stanovení těchto údajů uvádějí články [9, 10].
Závěr
Celistvost (robustnost, integrita) může být klíčovou vlastností moderních složitých konstrukcí. V současnosti je však mezi odborníky vnímána odlišně - někteří chápou celistvost jako schopnost konstrukce chovat se přiměřeně v mimořádné situaci, zatímco jiní jako schopnost systému, jehož součástí je sledovaná konstrukce, působit přiměřeně při mimořádné situaci této konstrukce.
Ačkoliv je hledisko celistvosti důležitou součástí návrhu složitých konstrukcí, kvantitativní ukazatele i metody hodnocení celistvosti nejsou zatím sjednoceny. Důležitým krokem je přijetí vhodné definice celistvosti a jednoznačné stanovení následků, které mají být uvažovány. Ukazuje se, že metody analýzy rizik jsou vhodným nástrojem pro hodnocení celistvosti.
Numerický příklad naznačuje, že efektivnost opatření pro zajištění celistvosti může být ověřena s využitím analýzy rizik a poznatků teorie spolehlivosti a pravděpodobnostní optimalizace. Ve většině případů je důležité odlišit lokální a globální účinky uvažovaných nepříznivých jevů. Pro praktické uplatnění popsaných metod je rozhodující kritické stanovení přímých a nepřímých následků poruchy s ohledem na skutečné podmínky sledované konstrukce.
Poděkování
Příspěvek byl vypracován v Kloknerově ústavu, ČVUT v Praze, v rámci řešení projektu COST OC08059 Hodnocení robustnosti stavebních konstrukcí podporovaném Ministerstvem školství, mládeže a tělovýchovy ČR. V příspěvku jsou využity poznatky dosažené v rámci Akce COST TU0601 Robustness of structures.
Použitá literatura:
[1] Holický, M., Sýkora, M., Jung, K. 2010: Zásady hodnocení celistvosti konstrukcí při poškození - I, Stavebnictví, roč. IV, č. 09/2010, 59-61 s.
[2] Ellingwood, B. R., Smilowitz, R., Dusenberry, D. O. a další. 2007: Best Practices for Reducing the Potential for Progressive Collapse in Buildings, NISTIR 7396, USA: National Institute of Standards and Technology, 216 s.
[3] DS-INF 146. 2003. Robustness - Background and principles - Information, Danish Standards Association
[4] Bilčík, J. 2010: Robustné betónové konštrukcie, Stavebnictví, roč. IV, č. 02/2010, 56-59 s.
[5] Ang, A. H. S. & De Leon, D. 1997: Determination of optimal target reliabilities for design and upgrading of structures, Struct.Saf., roč. 19, č. 1, 91-103 s.
[6] Rackwitz, R., Lentz, A. & Faber, M. 2005: Socio-economically sustainable civil engineering infrastructures by optimization, Struct. Saf., roč. 27, č. 3, 187-229 s.
[7] Holický, M. 2009: Probabilistic risk optimization of road tunnels, Struct. Saf., roč. 31, č. 3, 260-266 s.
[8] JCSS. 2006. JCSS Probabilistic Model Code, Zurich: Joint Committee on Structural Safety
[9] Tanner, P. 2008: Development of risk acceptance criteria for the design of steel structures: Proc. EUROSTEEL 2008, Brussels: ECCS Southampton, 6 s.
[10] Trbojevic, V. M. 2009: Another look at risk and structural reliability criteria, Struct. Saf., roč. 31, č. 3, 245-250 s.
Související článek:
Zásady hodnocení celistvosti konstrukcí při poškozování - I.