Záchrana historického kamenného mostu u Poniklé
Při plánované rekonstrukci historického tříobloukového kamenného mostu bylo na základě provedeného diagnostického průzkumu rozhodnuto o jeho zbourání. Průzkum se však soustředil pouze na prokázání degradace materiálu bez dalšího statického posouzení. Vzhledem k historické hodnotě mostu se příslušné orgány pokusily dané rozhodnutí zvrátit. Byl proveden jednoduchý statický výpočet, který prokázal, že most je schopen po odstranění vad vyvolaných zatékáním vody do konstrukce dále sloužit. Bourání nakonec bylo zastaveno s tím, že se most bude rekonstruovat a zachová se jeho historická hodnota.

Úvod
Most u Poniklé (v okresu Semily) přes řeku Jizeru, který je situován na silnici č. II/290 u napojení na silnici č. I/14, je kamenný historický tříobloukový klenbový most. Jeho vznik souvisí se stavbou silničního spojení mezi Libercem a Trutnovem v polovině 19. století, která byla zahájena v roce 1847. Podle nepřímých dokladů se zdá nejpravděpodobnější, že most byl dostavěn nejpozději v roce 1853. V současné době tak jde o nejstarší dochovaný historický kamenný most na Jizeře. Nepochybně byl navržen některým ze zemských nebo krajských stavebních inženýrů jako moderní dopravní stavba v souvislosti s budováním systematické státní silniční sítě. Architektonické detaily parapetních zdí nebo stříšek zhlaví pilířů dokládají vysokou architektonickou kvalitu návrhu, která se stala neodmyslitelnou součástí krajinného rázu údolí Jizery. V letech 1936 až 1937 proběhla komplexní obnova mostu.
Vzhledem k nedávno plánovanému rozšíření mostu byla zpracována studie, ve které se uvažovalo s novým mostem. V této souvislosti byl realizován diagnostický průzkum, který se zaměřil na vlastnosti materiálu a měl potvrdit velkou degradaci materiálu s nutností původní most zbourat. Posléze byla zpracována projektová dokumentace ke stavebnímu povolení a výběrovému řízení na zhotovitele nového mostu. Po výběru stavební firmy mělo dojít ke zbourání mostu. Při provedeném statickém přepočtu mostu však bylo zjištěno, že napětí v klenbové konstrukci je menší než únosnost materiálu, most lze opravit a není tedy třeba jej zbourat. Po tomto zjištění se vyvinulo značné úsilí a tlak na příslušné orgány i vlastníka, aby se most zachoval. Jednalo se o odbornou veřejnost (Fakulta stavební ČVUT v Praze) i informační zdroje (noviny a TV). To se nakonec podařilo a bourání bylo na poslední chvíli zastaveno, přestože již bylo odstraněno jedno pole zábradlí. Most byl Ministerstvem kultury prohlášen za kulturní památku a vlastník, Liberecký kraj, se zavázal k jeho šetrné obnově. Nezanedbatelným přínosem zachování mostu je vedle záchrany kulturního dědictví také úspora emisí CO2. Destrukce oblouků a částí pilířů by vedla k cca 230 m3 odpadu, navíc značné historické ceny. Objem nové konstrukce by byl u oblouků 148 m3, u části pilířů 95 m3, u zdí 33 m3 a mostovky 163 m3. Postavení nového mostu by tak vedlo k produkci přibližně 200 t CO2. Dalším důležitým hlediskem je životnost. Kamenné klenby jsou staré 170 let a navzdory zanedbané údržbě mostovky stále slouží. Při odpovídající ochraně proti zatékání vody mohou sloužit déle než plánované konstrukce železobetonové.
Předpoklady a cíle výpočtu
Pro zděné obloukové mosty je k dispozici množství metod posuzování, přesto neexistuje žádný obecně uznávaný rámec pro jejich použití [1]. V praxi je nutné zvolit metodu posuzování, která může využívat údaje dostupné v běžném návrhovém prostředí a s přiměřenými náklady. To připouští relativně jednoduché materiálové modely. Na druhou stranu není důvod vyhýbat se metodě konečných prvků, protože dokáže modelovat součásti mostu a jejich interakce způsobem, který jiné metody a kódy (modifikovaný MEXE, teorémy plasticity jako Ring [2], Castiglianův teorém jako kód CTAP [3] a další) nedokážou. K prokázání zatížitelnosti mostu byly vytvořeny tři nezávislé modely. Jeden podrobný v 3D pomocí prostorových FEM prvků ve statickém programu RFEM Dlubal. Dva zjednodušené v 2D, jeden fyzikálně lineární a jeden s fyzikální nelinearitou. Ve výpočtech byl uvažován násyp, který roznáší zatížení od pojezdu automobilů. Bylo zpracováno i posouzení podle EN 1991-2 (výpočet zatížení na mostech) a 1996-1-1 (posouzení zděných konstrukcí). Dalším cílem 3D výpočtů bylo zjistit, jestli lze počítat most zjednodušeně, resp. pouze jedno pole s 2D prvky. Po porovnání výsledků s prostorovým modelem se získal korekční součinitel pro 2D model.
Hlavní poruchou kamenných obloukových mostů jsou tahové trhliny v ložných spárách, které vedou k postupnému vzniku virtuálních kloubů, ke kterému dochází i při provozním zatížení. Předpokládá se, že malta v ložných spárách má zanedbatelnou pevnost v tahu, a proto se uvažuje materiál s vyloučením tahu. V klasickém kontinuálním modelu
z 2D a 3D prvků i s ortotropním materiálem však nelze jednoduše dosáhnout předurčené orientace trhlin. To by bylo nutno zvolit model, který je složen z jednotlivých kamenů s kontaktními nelineárními prvky.
Modely
Bylo vytvořeno několik modelů.
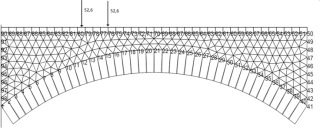
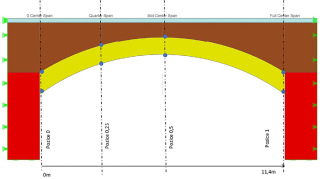
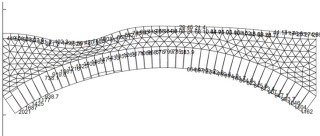
- 3D model s prostorovými prvky (brick). Pro ověření byl vytvořen model celého mostu včetně pilířů a opěr. Pohled na most a jeho 3D model metodou konečných prvků je zobrazen na obr. 1 a 2. Všechna rozpětí mají přibližně 11,4 m, plná šířka mostu je 7,6 m. 3D model o jednom rozpětí je výsekem celého mostu odděleného rovinami symetrie sousedních pilířů. Na tyto roviny jsou aplikovány okrajové podmínky symetrie (nulové normálové a volné posuny v rovině). Prvky jsou v podstatě izoparametrické cihly/čtyřúhelníky obohacené o rotační stupně volnosti ve všech uzlech. Používá se komerční program RFEM společnosti Dlubal Software.
- 2D model jednoho pole s vyloučeným tahem v ložných spárách klenby. Podmínky požadované normami se kontrolují v nelineárním 2D modelu (rovinná deformace) jednoho pole s výše uvedeným materiálem. V patkách klenby je pružné podepření, které umožňuje rotaci průřezu.
- Roztažení klenby při lokálním normovém zatížení zkoumaného pole dopravou, viz podkapitola Výpočet korekčního součinitele a roztažení klenby, se uplatní jako vynucené posunutí pravé omezující linie modelu. Výsledky jsou mírně zkresleny 2D idealizací, která zanedbává všechny příčné účinky, a omezenými vodorovnými posuny pružin. Oblouk je modelován nejjednoduššími přímými Timošenkovými konečnými prvky tak, aby byla zohledněna smyková deformace. Pro usnadnění kompatibilního připojení k 2D modelu kontinua výplně jsou standardní tři uzlové stupně volnosti (DOF) nosníkových Timošenkových prvků, dvě translace a jedna rotace nahrazeny třemi translačními DOF. Dva z nich jsou přiřazeny hornímu bodu koncového průřezu. To umožňuje bezproblémové spojení s jednoduchými trojúhelníky s konstantní deformací nebo izoprametrickými čtyřúhelníkovými prvky oblasti výplně. Třetí DOF uzlu je složka ve směru osy nosníku spodního konce čelního průřezu. Prvek je tedy „hybridem“ 1D nosníkového a 2D spojitého prvku.
Zkušenosti potvrdily, že v nelineárních úlohách tento prvek urychluje konvergenci iterací ve srovnání s klasickými nosníkovými prvky s rotačními DOF. Předpoklad tuhých průřezů umožňuje explicitní integraci normálového napětí přes průřez do nosníku v uzavřeném tvaru. Není nutná žádná numerická integrace. Materiálový model je nezávislý na historii (hyperelastický), takže není třeba ukládat žádné stavové proměnné. Tento prvek je nejjednodušší možný pro modelování vývoje trhlin v ložných spárách kamenných zděných oblouků. Úplný popis prvku a vzorce pro uzlové síly a matice tuhosti prvků lze nalézt v [4]. Řešení pro jeden oblouk kamenného zděného mostu je zakódováno v samostatném skriptu Octave/Matlab. Data pro jednotlivé úlohy se dodávají úpravami vstupní specializované funkce. Pro některé geometrie oblouků jsou k dispozici šablony, vytvoření sítě je pak automatické pomocí open source generátoru sítí [5]. K dispozici je jednoduchý, čistě vektorový grafický výstup. V grafickém výstupu je zobrazena deformovaná síť, (algebraická) minimální napětí v jednotlivých prvcích oblouku a hloubky trhlin v ložných spárách. Hodnoty napětí jsou vloženy na ploše (nahoře/dole), kde se vyskytují minima, zatímco hloubky trhlin jsou prezentovány v grafické podobě.
- 2D model jednoho pole – lineární a s vyloučením tahu. Používá se komerční program RFEM společnosti Dlubal Software. Modely slouží především k posouzení rozdílů mezi 2D a 3D výsledky a k vývoji korekčních faktorů, které lze použít pro výsledky získané z 2D řešení.
Materiálové vlastnosti
Norma EN 1996-1-1 poskytuje podporu pro stanovení pevnosti zdiva v tlaku kolmo k ložným spárám na základě pevností klenáků a spárové malty. Zkoušky byly provedeny pro zděné pilíře a oblouky mostu a byla stanovena návrhová pevnost v tlaku fd =2 MPa. Tato hodnota je spíše konzervativní, protože pískovcové kvádry jsou v dobrém stavu. Násyp a dlažba jsou uvažovány lineárně pružné. Pokusy o posouzení porušení násypu použitím Mohr-Coulombova modelu a dalších materiálových modelů jsou v akademické obci časté, ale v projektové praxi se téměř nikdy neuplatňují. Neexistuje téměř žádný způsob, jak získat parametry pro tyto materiálové modely. Totéž platí pro modely potenciálního porušení kontaktu mezi výplní a klenbou oblouku. Model předpokládá, že nosnou konstrukcí je klenba kamenného zdiva a lokální poruchy zásypu nemají vliv na zatížení, které musí klenba nést. Pro kontrolu rozsahu těchto poruch se v prvcích náspu porušení Druckerovy-Pragerovy podmínky vyznačuje hvězdičkami. Používá se nulová koheze a úhel vnitřního tření kolem spodní hranice hodnot uváděných v literatuře. Materiálové vlastnosti použité v modelech FEM jsou shrnuty v tab. 1. Materiálové hodnoty násypu jsou konzervativní, což lze zjistit i z [6].
Zatížení
Proměnné zatížení
Poloha sil ve čtvrtině rozpětí klenby je obecně považována pro oblouk za nejnepříznivější. Rozhodující je model zatížení LM1 podle normy EN 1991-1-1. Ve všech výpočtech se uvažuje stejná poloha obou nápravových tandemů, jak je znázorněno na obr. 2 a 4. Rovnoměrná zatížení LM1 nejsou na obrázcích znázorněna, ale ve výpočtech se uplatňují na zatížené polovině rozpětí. Za zmínku stojí, že LM4, 1 800 kN normy EN, dává přibližně stejné celkové zatížení na polovinu rozpětí, ale je lépe rozloženo.
Stálé zatížení
Stálé zatížení je reprezentováno vlastní tíhou konstrukcí.
Součinitelé zatížení
Součinitelé zatížení mezního stavu únosnosti jsou použity podle EN a národního aplikačního dokumentu. Zatížení ve 2D modelu je zprůměrováno z 3D zatížení na šířku mostu.
Výpočet korekčního součinitele a roztažení klenby
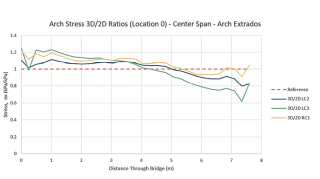
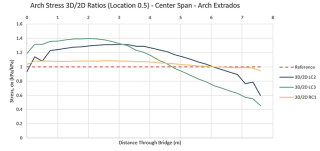
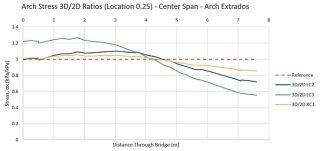
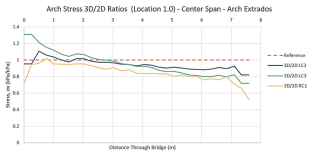
Aby bylo možné porovnat výsledky mezi 2D a 3D modely, bylo nutné při přípravě modelů dbát na dodržení stejných materiálů a zatížení. Pro určení poměrů a rozdílů ve výsledných hodnotách musela být místa zkoumaných hodnot stejná. V obr. 5 jsou zobrazena místa, kde bylo možné výsledky extrahovat a porovnávat. Body podél dolní (líc) a horní (rub) strany oblouku byly uvažovány v patě oblouku ve vrcholu a ve čtvrtinovém rozpětí podle předpokládaných míst vývoje plastických kloubů. Správně by se měla porovnávat normálová napětí v rovinách průřezu (roviny ložných spár). Software však nenabízí výstup těchto napětí. Místo toho se tedy porovnávají normálová napětí ve směru x. Hodnoty se mohou značně lišit, ale předpokládá se, že poměry 2D/3D jsou přibližně stejné. Grafické znázornění porovnání je uvedeno na obr. 6 pro tři zatěžovací stavy. Důležité pro konečné korekční součinitele jsou právě křivky RC1, které zobrazují napětí pro plná návrhová zatížení. Ostatní křivky jsou pro jednoduché zatěžovací stavy s charakteristickými součiniteli zatížení. Byly použity pro kontrolu konzistence výsledků 2D. Referenční hodnoty pro vyhodnocení korekčních součinitelů jsou vyznačeny čárkovanými vodorovnými čarami.
Data získaná z analýz konečných prvků vykazují určité nepravidelnosti, které jsou vlastní všem modelům konečných prvků. Například křivky v místě 0 a 1 (paty oblouků) na obr. 6 vykazují nepravidelné kolísání napětí na okrajích klenby – to je důsledek diskretizace. V těchto místech by „přesné“ řešení kontinua poskytlo nekonečná napětí vzhledem k ostrým konkávním rohům. Diskretizovaný model FEM se přibližuje „přesnému“ modelu a vytváří tyto fluktuace. Data byla proto dále průměrována, aby se získaly konečné vyhlazené diagramy na obr. 6. Korekční faktory byly odvozeny pro konkrétní prostorové parametry a materiálové vlastnosti mostu v Poniklé. Z autorova průzkumu [6] vyplývá, že mosty z období industrializace vykazují poměrně podobné parametry. Všechny oblouky mají přibližně stejné poměry stoupání/rozpětí a šířka/rozpětí, zásyp je vždy nesoudržná zemina se značným obsahem kamene. Tyto podobnosti opravňují k použití korekčních součinitelů i při posuzování podobných mostů. Kromě korekcí 2D modelu na změnu napětí v celé šířce mostu (3D) je pro model s jedním polem nutná korekce na interakci/poddajnost sousedních polí. Když je střední rozpětí zatíženo návrhovým zatížením, pilíře a sousední rozpětí jsou stlačena, takže se střední oblouk roztáhne. Roztažení je třeba posoudit a případně zohlednit korekcemi 2D nelineárního modelu. Nejjednodušším způsobem, jak to provést, je vložit posun získaný z modelu celého mostu jako vodorovný posun okrajové roviny. Vzdálenost rozšíření u = 0,12 mm byla vypočtena jako rozdíl vodorovných posunů levého a pravého oblouku ve středním poli. Ty jsou vzaty jako průměry posunů horního a dolního bodu v patě oblouku. Poněkud překvapivě mají vodorovné posuny horního a dolního bodu opačná znaménka. To je způsobeno převažující rotací nad posunem uložení klenby v pilířích. Model na obr. 2 se používá pro posouzení celého mostu.
Výsledky posouzení
Řešení mostu Poniklá pro návrhová zatížení je znázorněno na obr. 7 s nápravovými tandemy na čtvrtině rozpětí oblouku. Hodnoty napětí z obr. 7 se v posledním kroku vynásobí korekčními faktory z tab. 1. Most je bezpečný v mezním stavu únosnosti definovaném v normě EN 1991-1.
Závěry
Posouzení mostu Poniklá podle dostupných norem bylo předáno vlastníkovi mostu. Spolu s aktivitami dalších organizací a jednotlivců v oblasti ochrany kulturního dědictví pomohlo odvrátit demolici mostních oblouků. Památka na řemeslnou zručnost předchozích generací tak zůstala zachována pro naše potomky. Pro kamenné zděné oblouky byl vyvinut jednoduchý materiálový model a specializovaný konečný prvek, který lze použít k ověření složité konstrukce podle dostupných normových podmínek. Ve vývoji je rozšíření nelineárního modelu na 3D. Paralelní lineární 3D model pak nebude nutný. Aplikace na další obloukové kamenné mosty je jednoduchá.
Poděkování
Článek vznikl za podpory projektu NAKI DG20P02OVV001 (Nástroje pro zachování historické hodnoty a funkce obloukových a klenbových silničních mostů) Ministerstvo kultury České republiky.
|
E [GPa] |
G [GPa] |
ν |
ρ [t/m2] |
|
| Vozovka | 31,0 | 12,917 | 0,20 | 2,5 |
| Podsyp | 0,1 | 0,040 | 0,25 | 2,2 |
| Násyp | 0,1 | 0,043 | 0,15 | 1,8 |
| Klenba | 10,0 | 5,000 | 0,25 | 2,0 |
| Pilíře | 10,0 | 4,000 | 0,25 | 1,8 |
|
Poměrná poloha řezu |
|||||
|
0 |
0,25 |
0,5 |
1 |
||
|
Deformace ux, dolní líc |
min. |
0,55 |
0,85 |
0,92 |
0,59 |
|
max. |
0,90 |
1,00 |
1,02 |
0,92 |
|
|
Deformace ux, horní líc |
min. |
0,55 |
0,85 |
1,14 |
0,63 |
|
max. |
1,05 |
1,00 |
1,25 |
0,95 |
|
|
Napětí σx, dolní líc |
min. |
0,95 |
0,88 |
0,98 |
0,69 |
|
max. |
1,18 |
1,08 |
1,10 |
0,98 |
|
|
Napětí σx, horní líc |
min. |
0,96 |
– |
0,78 |
0,53 |
|
max. |
1,05 |
– |
0,94 |
0,55 |
|
|
Pozice |
Max. [kPa] |
Relativní [mm] |
Max. tlakové napětí s korekcí |
|
Levá podpora |
–1 576 |
0,22 |
–1 654,80 |
|
¼ rozpětí |
–1 107 |
0,15 |
–1 195,56 |
|
Vrchol klenby |
–713 |
0,00 |
–784,30 |
|
Pravá podpora |
–1 077 |
0,00 |
–1 141,62 |